Trigonometry - Sums with Stella
- Stella

- Aug 1, 2024
- 4 min read
Updated: Mar 23
Learn trig fast and demystifying Trigonometry – the word itself might sound intimidating, conjuring up memories of complex angles and equations. This article will help unravel the mysteries of trigonometry and guide you through the exciting world of triangles and angles.
Below are extra resources for you. Remember to subscribe on our website here or in the youtube channel and we will send you more useful information for FREE
 | |
 | |
 | Video Lesson 3 How to find an unknown angle using trigonometry. |
 | Video Lesson 4 Finding an angle of elevation or depression. |
 | Video Lesson 5 Bearings |
Introduction
Trigonometry is the branch of mathematics that deals with the relationship between the angles and sides of triangles. It has applications in various fields, from engineering and physics to astronomy and even art. By mastering the basics of trigonometry, you can open up a world of possibilities and enhance your problem-solving skills. Learn trigonometry fast.
We use trig when pythagoras theory is not possible.
To find a side we need at least one side and an angle.
To find an angle we need 2 sides
Getting Started: The Trigonometric Ratios (Sin/Cos/ Tan)
To calculate the angles and lengths, you need to first determine which formula or ratio to use. Each one has a different purpose.
Sin, cos, and tan are just ways to describe how big parts of a triangle are compared with each other. They are all about right triangles (triangles with a 90° angle).
These ratios define the relationship between the angles and sides of a right angled triangle. Let's break them down:
Sine (sin): The sine of an angle in a right triangle is the ratio of the length of the side opposite the angle to the length of the hypotenuse.
Cosine (cos): The cosine of an angle is the ratio of the length of the adjacent side to the length of the hypotenuse.
Tangent (tan): The tangent of an angle is the ratio of the length of the side opposite the angle to the length of the adjacent side.
Practical Application: Solving Triangles
Now that you understand the basic trigonometric ratios, let's put them to use in solving triangles. Given an angle and a side length in a right triangle, you can use trigonometry to find missing side lengths or angles. This process, known as trigonometric solving, is a fundamental skill in trigonometry.
Step 1: Identify the sides of a triangle
Step 2: Choose the correct formula (trig function)
Step 3: Solve the equation
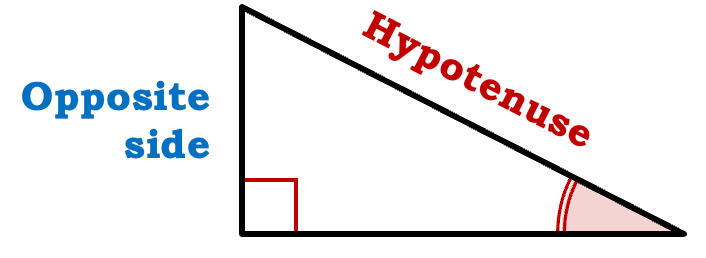
Lesson 1: Identify and label the sides of a triangle
Every angle will have a matching ratio and every ratio will have a matching angle
Step 1: A square will indicate the right angle of the triangle. | |
Step 2: Label the side opposite the right angle (the square) "Hypotenuse" | |
Step 4: Label the side opposite to the angle the "Opposite" side | |
Step 5: Label the remaining side the "Adjacent" side |
Lesson 2: Finding which formula to use
Calculate the unknown sides of a right angled triangle
Key Concepts to Remember
SOH-CAH-TOA : A mnemonic device to remember the trigonometric ratios – Sine = Opposite/Hypotenuse, Cosine = Adjacent/Hypotenuse, Tangent = Opposite/Adjacent.
Pronounced: "So-Ka-Toe-Ah" - remember this!!!
Unit Circle : An essential tool in trigonometry that helps visualise angles, values of trigonometric functions, and trigonometric identities.
Lesson 3: Finding unknown angles of a right angled triangle
Lesson 4: Angles of Elevation and Depression
Angles of elevation and depression are concepts in trigonometry that describe the angles formed between a horizontal line and an observer's line of sight to an object. The angle of elevation occurs when an observer looks upward at an object above the horizontal line; it's the angle between the horizontal and the line of sight. Conversely, the angle of depression is formed when an observer looks downward at an object below the horizontal line; it's the angle between the horizontal and the downward line of sight.
These angles are commonly used in real-world applications, such as determining the height of a building or the distance of a ship from a lighthouse. By applying trigonometric ratios—sine, cosine, and tangent—one can calculate unknown distances or heights when at least one side length and an angle are known
Lesson 5: Bearings
In trigonometry, bearings are used to describe the direction of one point relative to another, measured clockwise from the north direction. This system is essential in navigation, surveying, and various real-world applications. Bearings are typically represented as three-figure angles; for example, an angle of 45 degrees is written as 045°. Understanding and calculating bearings allow for precise navigation and positioning, which are crucial in fields such as aviation, marine travel, and land surveying.
Mastering Trigonometry
To excel in trigonometry, practice is key. Work through problems, delve into real-world applications, and explore the beauty of trigonometry in nature and architecture. Here are some tips to enhance your trigonometry skills:
Practice : Regular practice with trigonometry problems will help reinforce your understanding of concepts and improve your problem-solving abilities.
Engage with Resources : Dive into online tutorials, textbooks, and interactive tools to deepen your knowledge of trigonometry.
Real-World Applications : Explore how trigonometry is used in fields like engineering, architecture, and physics to appreciate its practical significance.
Conclusion
Trigonometry, often feared for its complexity, is a fascinating branch of mathematics with diverse applications in various fields. By understanding the basic concepts of trigonometry, you can unlock a world of possibilities and enrich your mathematical skills. Embrace the challenge, practice diligently, and soon you will find yourself navigating the world of angles and triangles with confidence and ease. Let sums with Stella help you learn trigonometry fast. We call it easy trig!!
Remember to keep exploring, learning, and challenging yourself – trigonometry is just the beginning of a mathematical adventure waiting to unfold.
.png)











Comments